Quark theory
Correlation of Proton Mass with Electron Mass
This article has been submitted to "Nature" but
was not accepted for publication. Nevertheless, no changes
were deemed necessary since the date of publication. An
experimental verification to the Moebius loop structure
of the High Energy Lepton forming the quark has been proposed
in the article on the electron.
Updated 1.4.2023 since its posting on my homepage
Dr. Christoph Caesar[1]
Munich
One of the key questions of elementary
particles physics is the mass relation between leptons and
nucleons or quarks. Leptons in many hadron decays and interactions
show a typical energy of 53 MeV. Explicit numbers of these
electrons accommodated in a quark fit the observed mass
and charges of quarks and nucleons. The model further is
shown to have exactly and only three different variations
for quarks, the colours.
The success of QED and QCD in describing
interactions of elementary particles and in predicting results
of measurements performed with quantum-wave particles is
unquestioned. Still missing, however, is a physical description
or model of the elementary properties, e.g. the "color"
of a quark or the "charge" of a quark or of an electron.
A quantum reality[1]
is searched for which could e.g. reduce the number of elementary
constants (now approx. 20) or reduce the number of elementary
forces. If it could solely be achieved to correlate properties
like masses of the electron and nucleons, it would be regarded
as major progress[2],[3].
Some Existing Quark and Nucleon Models
There are some models to unify leptons and quarks by a
preon or rishon model. The "rishon" model of H. Harari[4]
tried to explain all elementary particles as compositions
of three rishons and their antirishons. A similar preon
- model of Salam and Pati[5]
consists of "somons", "flavons" and "chromons" with several
variations and electrical charges between +/-1/2 and +/-
1/6. These models, however, open a new and complicated "particle
zoo" instead of simplifying physics. Both models have not
overcome the "mass paradox", i.e. that the sum of all rishon/preon
masses does not fit to the sum of the constituents plus
the corresponding binding energy.
A clue for a step towards a correlation between hadrons
and leptons could be certain particle reactions, where electrons
and even neutrinos of up to 53 MeV are produced[6]
- e.g. the pion/myon decay. Usually it is denied that nucleons
or mesons really "contain" electrons[7],
but these high energy leptons have little in common with
charge clouds that form the orbit around a hydrogen atom.
A highly energetic and agitated state is expected to be
the result of the decay of the two-quark pion. What, if
nucleons and pions really contain 53 MeV leptons? It is
remarkable that eighteen times 53 MeV approximately gives
the nucleon mass.
Quark and Nucleon mass
As a working hypothesis for the structure of a quark a
single spherical quantum wave is assumed. It should have
a mass of around 300 MeV, a spin, show exactly three different
configurations, the "colors", and should exhibit the well
known +/-1/3 or -/+ 2/3 charges. A single quark then would
be an unstable rotating (spin) spherical wave aggregate;
two of them should form the relatively stable pions. Three
of them each form the proton with 938 MeV and the neutron
with 940 MeV. The particle decays and reactions of course
would have to be the ones successfully described by QCD
and QFT.
The nucleon consists of three quarks. 3 times 6 = 18 of
these 53 MeV leptons amount to 954 MeV which is very close
to the proton mass; six 53 MeV leptons therefore might generate
or inhabit one quark of 318 MeV, e.g. orbiting each other
in the spherical wave. In an atomic nucleus, 8 MeV are necessary
for removing one nucleon[8].
Applying this binding energy also to a quark, this would
give a total binding energy of 2 * 8 MeV to remove two of
three quarks. 954 MeV minus binding energy now should give
the nucleon mass:
6 * 3 * 53 MeV
- 2* 8 MeV = 938 MeV
qed
The value "938 MeV" had to be proven (qed "quod
erat demonstrandum" in Latin) and it is the expected
result.
The free neutron, as it is unstable, simply would have
to have a slightly smaller binding energy of 7 MeV per quark
to yield the observed 940 MeV.
This approach for the first time would correlate lepton
mass with nucleon mass. The question is, why and how exactly
six lepton orbits should be accommodated in the quark. The
poles of a spherical wave are crossed diagonally by one
lepton each and this scheme can be applied to every crossover
of a meridian crossing the equator or another meridian as
shown in Fig. 1. Exactly and only six different and independent
orbits of this type can be drawn in and are given as single,
double and triple lines and as solid or broken lines, respectively,
comparable to the Pauli Exclusion Principle.
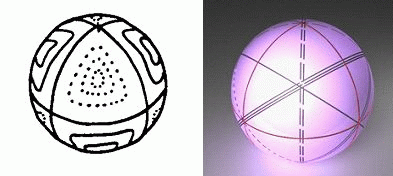
Fig. 1: The quark as spherical wave. Left:
quantum wave by Herbert10; right: spherical wave occupied
with six individual orbits
If each of these orbits is occupied with only one lepton
they form a quark. Filling each orbit with a lepton pair
with antiparallel spin, then twelve leptons minus binding
energy would give a two-quark particle with much higher
stability, e.g. a pion. The two-quark pions, e.g. the u-d-bar,
then consist of 2*6 = twelve high energy leptons. The pion
mass of only 135 to 140 MeVs hardly fits into the 318 MeV
scheme per quark - they should have a mass of 636 MeV minus
some binding energy. But three quarks perfectly form the
stable nucleon with a reasonable binding energy; hence the
naked quark is completely unstable and never has been observed
alone. A two quark pion is fully charge- and spin compensated
and therefore it is relatively stable. Höfling[9]
attributes the total spin compensation to spin 0 to a very
high binding energy between the two quarks and explains
the low pion mass in this way, too. The simplest second
generation particles - the negative and positive myons -
have a mass of 106 MeVs, exactly twice that of the high
energy nucleus electron.
Quark partial charges and colors
To account for the quark charges of -1/3 and +2/3 of the
elementary charge it was tried to find a scheme where the
electric charge of these particles could be formed by a
composite, which contains common fractions of the total
electrical field ranging from - 2/3 over - 1/3 to + 1/3
and +2/3 charges. The system then accommodates the seven
possibilities from -3/3 to + 3/3, as given in table 1:

Table 1 Scheme of leptons and quarks sorted by their charges
The simplest spherical wave to fit these seven variations
is the same sphere as in Fig. 1 divided into 8 quadrants
by two meridians and one equator. This version of the wave
function often is shown as agitated state of a spherical
quantum wave - e.g. as described by Herbert[10].
The -1/3 and + 2/3 charges can be built with the common
factor of +/-1/6 elementary charge per quadrant. The 1/6th
charge also is a component of the model of Salam and Pati[11].
A sphere with three positive and five negative 1/6 charged
quadrants has a total balance of 3/6 -5/6 = -2/6 = -1/3,
which corresponds to the charge of the down-quark. A sphere
with 2 negative and 6 positive quadrants has 6/6 -2/6 =
4/6 = + 2/3 charge and relates to the up-quark charge. An
antiquark easily is identified as having e.g. five positive
and three negative quadrants to form the anti-down-quark
or d-bar. Two positive and six negative fields can then
form the -2/3 charge of the anti-u / u-bar.
This result with a well known oscillation state of a spherical
wave now would have to account for the three colors of the
quarks. There are many possible permutations how the eight
quadrants can be polarized in groups of six positive and
two negative or three positive and five negative quadrants.
A simple scheme consisting of a table of the 8 quadrants
of the down quark was drawn, where every possible combination
of 3+ and 5- segments is indicated. Table 2 represents the
first combinations. The upper row shows the "northern" hemisphere
opened like a world map, the lower row the "southern" hemisphere.
Imagining a ball with three positive fields on the northern
hemisphere, number 2 and number 3 are equal to number 1
by rotation, no. 5 equals no.1, looking on the pole, too
and so on.

Table. 2: The first possible combinations of segment polarities
of the d-quark.
It is found that only three different versions of the down
quark exist, all variations can be rotated into one of the
marked three arrangements of table 2. The bold marked variations
cannot be derived by rotation or symmetry from each other.
Fig. 2 shows the three - dimensional schematic of the identified
d-quark versions.

Fig. 2: The three possible configurations
of the Down - Quark.
The same procedure was performed on the up-quark with two
"-" and six "+" fields. Again, only three variations were
found, which cover all possible permutations of the 2/6
quark.

Fig. 3: The three possible configurations
of the Up-Quark.
These three and only variations can be christened red,
green and blue and perfectly match the three different colors
in which the quarks are known. With these three variations
the current model easily can explain the three colors of
the quarks in QCD. The colors were originally introduced
to avoid a violation of the Pauli Exclusion Principle and
can now be simplified from a theoretically required, abstract
quantum number to a real variation of quadrant polarity
distribution. With this success of the concept to explain
charges and colors, one quark can be regarded as sphere
of waves with eight quadrants with specific polarities of
1/6 e each.
The other combinations of field distributions of the eight
quadrant spheres now consist of:
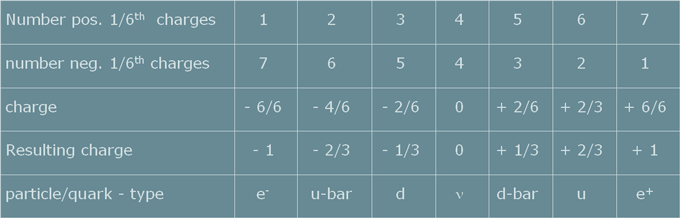
Table 3: first generation particles
The simplicity of this scheme is appalling. With all variations
of a simple agitated state of a spherical wave, the basic
elementary particles - as taking part in hadron reactions
- can be described. With a 1:7 ratio of positive and negative
quadrants, even an electron- and a positron - like quark
can be identified. It is not assumed that the normal state
of the free electron always is of this type, but definitively
a state of the spherical quantum wave the electron could
obtain at high energies can be composed in this way. The
neutrino also is known to be emitted with energies up to
53 MeV. The +4/6 -4/6 sphere then could be called a neutrino-like
quark. It should also be able to emit photons until it achieves
the "hardly visible" status known as neutrino. "This
means that neutrino and antineutrino are identical particles.
The starting point is the Dirac equation." - see [18].
These quark-like leptons are emitted as highly energetic
beta - particles from the nucleus in a decay process. They
stepwise achieve lower energetic states by photon emission
until they can be regarded as "normal" free leptons. This
radiation is observed as the Cerencov radiation[12].
The process can be visualized as in Fig. 4:
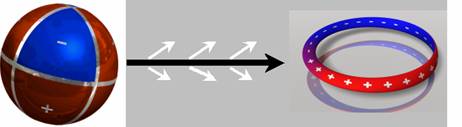
Fig. 4 Schematic decay of the 7/1 or positron quark into
the free positron
Nucleon Composition
These quantum wave spheres now should form the known particles.
The proton (uud) would consist of:

The partial charge balance of the
neutron n = udd would be:

Open is still, in which manner the
three quark spheres interact to form a nucleon. Three spheres
grouped together by electrostatic forces do not fit to the
extremely strong color forces observed - and the single
quarks never have been observed alone.
Within the proton and the neutron
the distribution of the electric field and the corresponding
magnetic field should be visible depending on the radius
and it should represent the different kind of quarks and
their spin. The internal charge distribution of the nucleons
found in the 50ies by Hofstadter et al. [13],[14]
would suggest three spheres nested one within the other
and thus continue the self - similar structure of the electron
shell of the atom, the shell - like structure of atomic
nuclei to a shell structure of the nucleons themselves.
There are six 53 MeV leptons per
quark, as only six different stable orbits per sphere are
possible. A total of six leptons passing 4 fields per revolution
gives 24 fields. The proton consists of 3 quarks with 8
quadrants each, i.e. 24 fields, too, which could in some
way account for the high stability of the proton. Of these
24 fields there are 15 positively and 9 negatively charged
quadrants. There is a balance of +15 - 9 = 6 positive fields
in excess. As the total proton charge is + 1 e, the assumed
charge per quadrant of 1/6 e per field is confirmed. The
fractional charge per quadrant could be interpreted like
in quantum mechanics, where charge often is supposed to
be shielded by virtual electron positron pairs. Due to the
high energy of the particles concerned, the shielding should
be significant and yield the 1/6 total visible charge per
quadrant of the quark. The orbiting lepton fields also could
partly compensate each other [15],
so that the average field gives one sixth e per quadrant.
Example reactions
The reactions or decay processes of elementary particles
shall - of course - be met by the model. One of the best
known examples is the decay of the free neutron[16]:
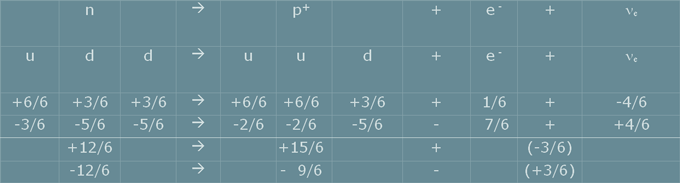
This is not only a charge balance
fitting accidentally or by implication, but quantitatively
gives the positive charge balance and the negative balance.
Additionally, the model shows the necessity for the reaction
to emit the neutrino for the individual charge balance of
each polarity.
The proton--> neutron reaction
in nuclear fusion is:

Again, the charge balance per polarity
is met and the neutrino emission is predicted as necessary
not only for momentum conservation, but also for lepton
charge conservation.
One example reaction already mentioned
is the decay of a (140 MeV plus impulse) pion (u d-bar)
into a myon (106 MeV) and a myon - neutrino and the subsequent
myon decay into a positron, an anti - myon - neutrino and
an electron - neutrino (overall reaction):
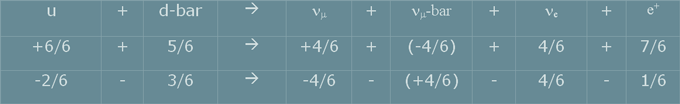
The positron charge here is identified
as +7/6 and -1/6 quark type particle. The antineutrino has
to be added with inverted polarities to account for the
charge and spin balance and the total balance perfectly
matches. It is confirmed again that a beta particle resulting
from a nuclear or high energy particle reaction can be described
as a agitated spherical wave with -/+ 7/6 and +/-1/6 charge
and that a high energy neutrino can be described as +4/6
and -4/6 = neutral quark. The law of charge conservation
obviously is valid also for the 1/6th charge
fields for each polarity separately.
Outlook for quantum mechanics
This approach correlates lepton mass with nucleon mass.
It also reveals the historical difficulties, as not the
ratio of (0.51/938) MeV, but a very specific high energy
state of the lepton of (53/938) MeV is relevant. We have
a model that accounts for the 1/3 charges and the three
colors of the quarks with a well known and simple state
of a spherical wave with different field polarities in eight
quadrants. Higher generation leptons and quarks are presumed
to be excited states of first generation leptons and quarks,
as also postulated by Harari, ref. [17].
The charge of the quark is the sum of the electromagnetic
field components of high energy leptons in eight quadrants.
It is postulated that the constituents of the quark - the
above mentioned high energy electrons and positrons - on
their orbits within the quark have their fraction of the
total charge located in one quadrant field of the sphere
and the remaining fields compensate each other inside or
on the backside of the sphere. All first generation particles
relevant in hadron reactions can be derived from the possible
variations of the polarity. The neutrino-quark is identified
as particle of a structure equivalent to the nucleon electron.
Its occurrence is demanded also for local charge balance,
not only for momentum conservation.
Questions and correspondence should be addressed to:
physics@ccaesar.com
[1]
Present address: Dr.-Ing. Christoph Caesar, Buschingstrasse
30, D-81677 München, Germany
[1]
Herbert, N. "Quantenrealität" Goldmann 1987, 32ff
[2]
Höfling, O., Waloschek, P., "Die Welt der kleinsten
Teilchen", rororo Sachbuch 8474, (1988), S. 455
[3]
Grotelüschen F., "Der Klang der Superstrings",
dtv, (1999), p. 30 ff , p. 75
[4]
Harari,
H.; "A
Schematic Model of Quarks and Leptons", Physics Letters
B, (1979) Vol. 86, No. 1, pp. 83-86
[5]
Pati,
J. C.; Salam,
A.; Lepton
number as the fourth "color", Phys. Rev. D (1974) 10,
275-289
[6]
Finn, Alonso, "Fundamental University Physics",
Addison-Wesley, Pub. .Co. (1968), 9.4 p.386
[7]
Höfling, ref. 2, p. 210
[8]
Cramer J. G. "Inside the Quark", www.npl.washington.edu/AV/altvw80.html
(1996)
[9]
Höfling, ref. 2, p. 431f
[10]
Herbert N., ref. 1. p. 124
[11]
Pati,
J. C.; Salam,
A. ref. 5
[12]
Höfling, ref. 2, p. 465
[13]
McAllister, R. W. & Hofstadter R., "Elastic Scattering
of 188 MeV Electrons from Proton and the Alpha Particle,"
Physical Review, V102, (1956) p. 851.
[14]
Hofstadter R., "The
Electron Scattering Method & its Application to the
Structure of Nuclei and Nucleons," Nobel Lectures, Physics
1942-1962, (1961) pp. 560-581, Elsevier Pub. Co., Amsterdam-London-New
York.
[15]
Caesar, C., „Electromagnetic Model of the Electron ", submitted
to Physical Review D, 2009
[16]
Höfling, ref. 2, p. 307
[17]
Harari,
H., http://en.wikipedia.org/wiki/Harari_Rishon_Model
(2008)

Web Counter by www.webcounter.goweb.de